Additional Exercises III - The Normal distribution

2.3. Additional Exercises III - The Normal distribution#

2.3.1. Exercise 1: Recall Statistics#

In order to apply AI algorithms, write codes and evaluate large data sets, we need some statistics.

Recall in groups the following topics:

  1. What is a normal distribution? What is a standard deviation, the variance, confidence intervalls?

  2. What kind of means are there?

  3. What is the central limit theorem

  4. What is the law of large numbers?

  5. What is linear regression?

  6. What is logistische Regression?

  7. What is a general linear model (GLM)?

  8. What is a Poisson distribution?

2.3.2. Exercise 2: Checking for Normal Distribution#

2.3.2.1. DWD data#

We begin by loading the meteorological data set from the Deutscher Wetterdienst DWD (German Weather Service) Open Climate Data Center . You find a documentation of this data in german and english.

# First, let's import all the needed libraries.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

dahlem_clim = pd.read_csv(
    "https://userpage.fu-berlin.de/soga/data/raw-data/NS_TS_Dahlem.txt", sep=";"
)
dahlem_clim.head(10)
STATIONS_ID MESS_DATUM_BEGINN MESS_DATUM_ENDE QN_4 MO_N MO_TT MO_TX MO_TN MO_FK MX_TX MX_FX MX_TN MO_SD_S QN_6 MO_RR MX_RS eor
0 403 17190101 17190131 5 -999.0 2.8 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999 -999.0 -999.0 eor
1 403 17190201 17190228 5 -999.0 1.1 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999 -999.0 -999.0 eor
2 403 17190301 17190331 5 -999.0 5.2 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999 -999.0 -999.0 eor
3 403 17190401 17190430 5 -999.0 9.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999 -999.0 -999.0 eor
4 403 17190501 17190531 5 -999.0 15.1 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999 -999.0 -999.0 eor
5 403 17190601 17190630 5 -999.0 19.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999 -999.0 -999.0 eor
6 403 17190701 17190731 5 -999.0 21.4 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999 -999.0 -999.0 eor
7 403 17190801 17190831 5 -999.0 18.8 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999 -999.0 -999.0 eor
8 403 17190901 17190930 5 -999.0 13.9 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999 -999.0 -999.0 eor
9 403 17191001 17191031 5 -999.0 9.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999.0 -999 -999.0 -999.0 eor

2.3.3. Exercise 2A: Subsetting the data frame#

First, we want to subset the entire dataset.

We only want to keep data from 1961 to day. Subset the entire dataset (not only 1 column as we saw in the seminar)! hwo many rows has the dataframe now?

### your code here ###

2.3.3.1. solution#

## you could do e.g.,:
dahlem_clim = dahlem_clim.loc[dahlem_clim["MESS_DATUM_BEGINN"] >= 19610101]
dahlem_clim.head(10)
STATIONS_ID MESS_DATUM_BEGINN MESS_DATUM_ENDE QN_4 MO_N MO_TT MO_TX MO_TN MO_FK MX_TX MX_FX MX_TN MO_SD_S QN_6 MO_RR MX_RS eor
2778 403 19610101 19610131 5 5.01 -1.02 1.31 -3.88 2.63 7.8 -999.0 -16.2 71.5 5 50.4 7.4 eor
2779 403 19610201 19610228 5 6.12 4.66 7.98 1.56 2.56 15.5 -999.0 -4.7 61.4 5 41.9 7.6 eor
2780 403 19610301 19610331 5 5.58 6.79 10.79 3.15 3.02 19.4 -999.0 -3.7 124.1 5 52.9 18.6 eor
2781 403 19610401 19610430 5 4.88 11.38 16.61 6.24 2.40 26.1 -999.0 -0.9 192.7 5 55.7 13.3 eor
2782 403 19610501 19610531 5 6.11 11.23 15.54 7.18 2.29 23.8 -999.0 3.0 132.8 5 120.1 26.7 eor
2783 403 19610601 19610630 5 4.39 17.73 23.18 11.47 2.12 30.4 -999.0 5.5 273.4 5 48.3 13.4 eor
2784 403 19610701 19610731 5 5.79 16.16 20.88 12.14 2.49 33.0 -999.0 8.8 143.2 5 72.6 13.2 eor
2785 403 19610801 19610831 5 5.34 15.97 21.20 11.40 2.40 28.5 -999.0 8.0 169.7 5 43.0 10.3 eor
2786 403 19610901 19610930 5 3.48 15.95 22.00 11.06 2.11 30.0 -999.0 4.4 201.7 5 35.5 12.1 eor
2787 403 19611001 19611031 5 4.77 11.10 15.54 7.26 2.39 22.3 -999.0 3.3 136.8 5 35.7 16.4 eor 
dahlem_clim.shape[0]  # number of rows

732

2.3.4. Exercise 2B: Checking the mean and standard deviation for this subset#

Calculate the mean and standard deviation for the monthly mean temperature! Doe they violate the three sigma rule? plot the distriubtion as histogram and density plot.

### your code here ###

2.3.4.1. solution#

np.mean(dahlem_clim.MO_TT), np.std(
    dahlem_clim.MO_TT
)  ## Yes it violates the 3 sigma rule!

(9.404439890710382, 6.846380527375167)

plt.figure(figsize=(10, 5))
plt.hist(dahlem_clim.MO_TT, bins="sturges", color="lightblue", edgecolor="grey")
plt.xlabel("Temp in °C")
plt.ylabel("absolute frequency")
plt.show()
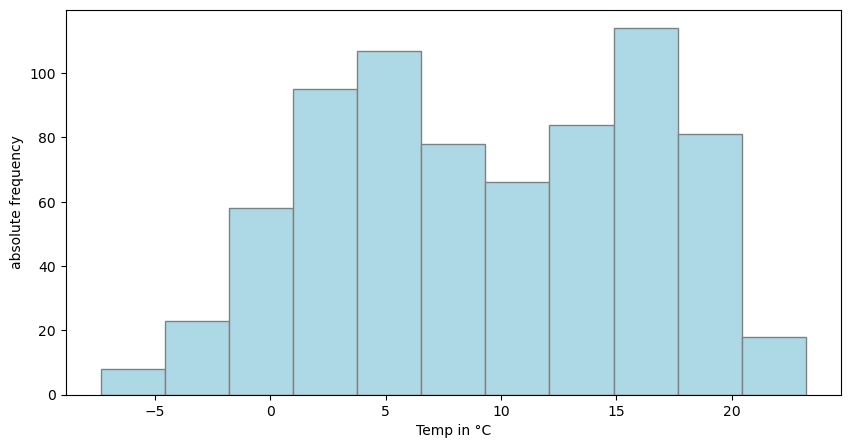
../../../_images/bedd031142fecbcd5ace070289ca6f4d4efc03b8581d5f5dede15238314665f7.png

Ok, looks Bimodal! But there seems to be no normal distribution…..

2.3.5. Exercise 2C: Checking the mean and standard deviation for this subset#

Check for normality of the monthly mean temperature with the help of a qqplot!

### your code here ###

2.3.5.1. solution#

import statsmodels.api as sm

plt.figure(figsize=(12, 5))
sm.qqplot(dahlem_clim.MO_TT, line="r")

plt.show()

<Figure size 1200x500 with 0 Axes>
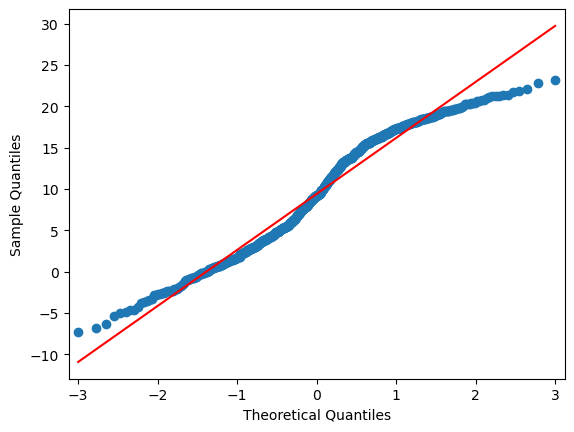
../../../_images/f521a6c643fdab944e1e41d3ec1fa9701744e5c0442b2c007c21dd0e77a8e17c.png

Well, we already suspected something like this…. Lets have a closer look:

2.3.6. Exercise 2D: Slicing the data frame#

Now, we want to slice the dataset into 2 parts. We want to subset between 1961 to 1990 and from 1991 to today. Subset the entire dataset (not only 1 column as we saw in the seminar)!

### your code here ###

2.3.6.1. solution#

## combined conditions :

dahlem_1961_1990 = dahlem_clim.loc[
    (dahlem_clim["MESS_DATUM_BEGINN"] >= 19610101)
    & (dahlem_clim["MESS_DATUM_BEGINN"] < 19910101)
]
dahlem_1961_1990
STATIONS_ID MESS_DATUM_BEGINN MESS_DATUM_ENDE QN_4 MO_N MO_TT MO_TX MO_TN MO_FK MX_TX MX_FX MX_TN MO_SD_S QN_6 MO_RR MX_RS eor
2778 403 19610101 19610131 5 5.01 -1.02 1.31 -3.88 2.63 7.8 -999.0 -16.2 71.5 5 50.4 7.4 eor
2779 403 19610201 19610228 5 6.12 4.66 7.98 1.56 2.56 15.5 -999.0 -4.7 61.4 5 41.9 7.6 eor
2780 403 19610301 19610331 5 5.58 6.79 10.79 3.15 3.02 19.4 -999.0 -3.7 124.1 5 52.9 18.6 eor
2781 403 19610401 19610430 5 4.88 11.38 16.61 6.24 2.40 26.1 -999.0 -0.9 192.7 5 55.7 13.3 eor
2782 403 19610501 19610531 5 6.11 11.23 15.54 7.18 2.29 23.8 -999.0 3.0 132.8 5 120.1 26.7 eor
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
3133 403 19900801 19900831 10 4.05 18.75 24.83 13.61 1.80 32.0 17.4 7.5 253.7 10 74.7 25.2 eor
3134 403 19900901 19900930 10 5.79 12.27 16.55 9.25 2.13 21.7 23.1 4.8 114.0 10 52.4 8.6 eor
3135 403 19901001 19901031 10 4.10 10.52 15.35 6.74 2.18 23.1 16.9 0.3 157.7 10 9.8 4.3 eor
3136 403 19901101 19901130 10 6.55 5.26 7.40 3.16 2.01 12.1 18.0 -2.4 47.3 10 56.6 16.4 eor
3137 403 19901201 19901231 10 6.04 1.13 2.84 -1.07 2.19 9.0 21.0 -5.8 41.2 10 73.0 23.3 eor

360 rows × 17 columns

## combined conditions:

dahlem_1990_today = dahlem_clim.loc[dahlem_clim["MESS_DATUM_BEGINN"] >= 19910101]
dahlem_1990_today
STATIONS_ID MESS_DATUM_BEGINN MESS_DATUM_ENDE QN_4 MO_N MO_TT MO_TX MO_TN MO_FK MX_TX MX_FX MX_TN MO_SD_S QN_6 MO_RR MX_RS eor
3138 403 19910101 19910131 10 4.97 2.30 4.57 0.07 2.16 15.2 18.5 -8.7 76.20 9 27.6 13.7 eor
3139 403 19910201 19910228 10 5.27 -2.34 0.85 -5.32 1.84 12.9 14.9 -12.9 72.40 9 27.1 7.9 eor
3140 403 19910301 19910331 10 4.79 6.77 11.30 3.25 2.15 18.1 14.4 -1.2 128.30 9 40.8 19.0 eor
3141 403 19910401 19910430 10 4.80 8.23 13.28 3.32 2.02 20.5 20.0 -2.8 174.80 9 40.4 7.8 eor
3142 403 19910501 19910531 10 4.97 10.52 14.90 5.90 2.19 24.2 24.1 1.2 179.60 9 38.6 15.5 eor
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
3505 403 20210801 20210831 3 5.67 17.43 22.34 12.97 2.42 29.4 16.9 8.0 188.23 3 92.4 22.6 eor
3506 403 20210901 20210930 3 4.90 15.55 20.28 11.35 2.33 27.3 18.6 6.8 154.48 3 35.1 15.9 eor
3507 403 20211001 20211031 3 4.85 10.49 15.28 6.29 2.81 24.2 25.6 0.5 157.65 3 21.8 5.7 eor
3508 403 20211101 20211130 3 6.65 6.28 8.68 3.87 2.60 12.7 18.6 -0.9 41.23 3 65.2 40.4 eor
3509 403 20211201 20211231 1 6.57 2.19 4.30 -0.11 2.74 14.0 21.5 -10.2 38.18 3 39.2 8.8 eor

372 rows × 17 columns

2.3.7. Exercise 2E: Checking for Normality#

Calculate the mean and standard deviation for the monthly mean temperature for both dataframes! Doe they violate the three sigma rule? plot the distriubtion as histogram and density plot. Check for normality of the monthly mean temperature with the help of a qqplot! (solution the same as above)

### your code here ###

2.3.8. Exercise 2F: Boxplots#

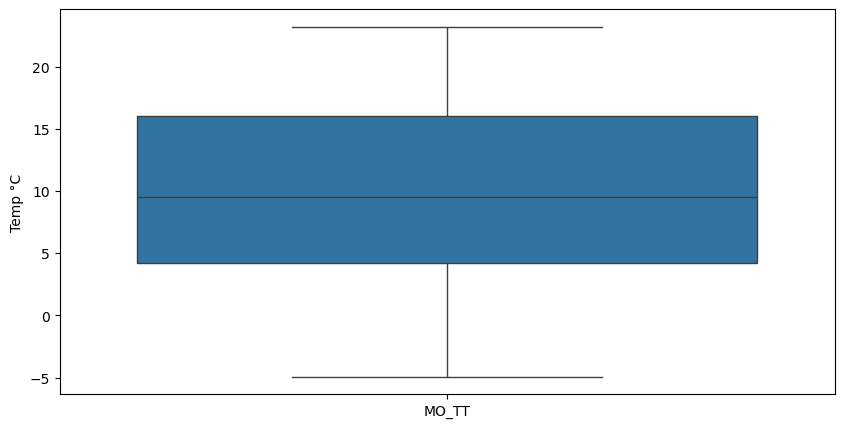
Let’s have a closer look at both dataframes with the help of a boxplot! Plot both datasets next to eachother in two boxplots but one figure frame.

### your code here ###

2.3.8.1. solution#

fig = plt.figure(figsize=(10, 5))

sns.boxplot(data=[dahlem_1961_1990["MO_TT"], dahlem_1990_today["MO_TT"]])

plt.ylabel("Temp °C")
plt.show()
../../../_images/c9510c9f592b1f40c5b90d37a94f99a45abbc89ee13e1bd61c8143cdb12c6d06.png

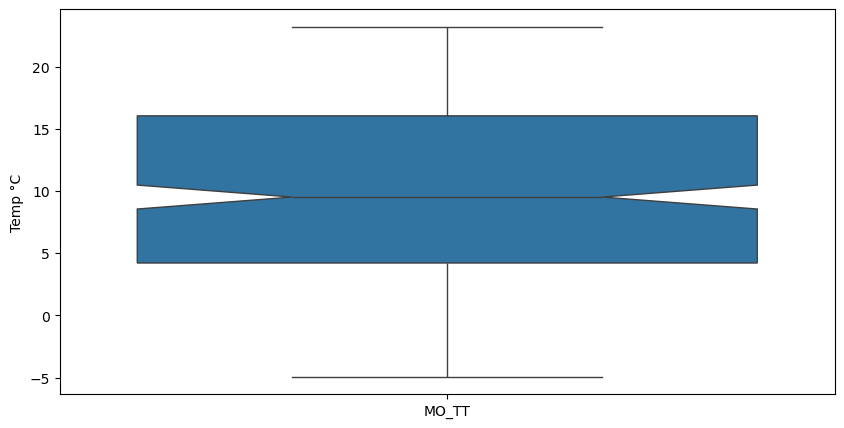
2.3.9. Exercise 2G: Nodges#

Which argument to we have to add, if we want to find significant differences between the groups? Is there a signifanct difference in the monthly mean temperature between 1961 to 1991 and from 1991 to today?

### your code here ###

2.3.9.1. solution#

fig = plt.figure(figsize=(10, 5))

sns.boxplot(data=[dahlem_1961_1990["MO_TT"], dahlem_1990_today["MO_TT"]], notch=True)

plt.ylabel("Temp °C")
plt.show()
../../../_images/1cfb827fd71c908b762f3962e3b6e34a05c7a2908c748310f778de1e83c91b1d.png 
from IPython.display import IFrame

IFrame(
    src="../../citations/citation_Marie.html",
    width=900,
    height=200,
)
Contents