2.1. Grundwasservorhersage mittels eines Random Forests, Hessen

author: Noura Barakat, Melvin Hildebrand

area: Hessen

date: 26.08.2024

## Erstmal importieren wir alle benötigten libraries

import os, sys
# import netCDF4
import pandas as pd
#import datetime
#from datetime import date, datetime, timedelta
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import xarray as xr
import geopandas as gpd
import rioxarray
import xarray as xr
import glob

import warnings
warnings.filterwarnings("ignore", "use_inf_as_na")

---------------------------------------------------------------------------
ModuleNotFoundError                       Traceback (most recent call last)
Cell In[1], line 11
      9 import matplotlib.pyplot as plt
     10 import seaborn as sns
---> 11 import xarray as xr
     12 import geopandas as gpd
     13 import rioxarray

ModuleNotFoundError: No module named 'xarray'

from io import StringIO
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_squared_error
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
import math
from math import sqrt

pwd = os.getcwd()
print(pwd)

C:\Users\nunub\OneDrive\Documents\KI_2024

2.1.1. Einlesen unserer vorverarbeiteten Daten

Wir verwenden hier bereits vorverarbeitete Daten. Der Datensatz umfasst Daten von einer Grundwassermesstelle (ID: 10319, Name: Lettgenbrunn) in Hessen. Zur Vorverarbeitung haben wir die .nc-Datei auf das AOI (Gebiet von Interesse) zugeschnitten und die .nc-Dateien für bestimmte Jahre zu einer Datei zusammengeführt. Dann haben wir Klimadaten (Temperatur- und Niederschlagswerte) an bestimmten Standorten extrahiert, sie mit GW-Pegel-Daten (Grundwasserpegel-Daten) zusammengeführt und die Daten für die Messtelle als einzelne CSV-Datei gespeichert. Diese Datei ist nun die Grundlage für den Aufbau unseres Modells.

Unser nächster Schritt ist der Modellaufbau.

data = pd.read_csv("./data/HYRAS_GWData_csv/HE_10319_weeklyData_HYRAS_GWData.csv", skipinitialspace=True).drop(['Unnamed: 0'], axis=1)

data.shape[0]

835

col2use = ['pr', 'tas', 'GWL']

#data = data.replace(np.inf, np.nan)
data.isnull().sum()

Date      0
pr        0
tas       0
GWL     148
dtype: int64

## hier werfen wir die Werte ohne Angaaben raus

data.dropna(axis=0, inplace=True)
data

	Date	pr	tas	GWL
148	1992-11-02	10.2	7.900000	371.92
149	1992-11-09	35.0	6.800000	372.46
150	1992-11-16	22.8	6.914286	373.40
151	1992-11-23	21.6	8.500000	376.69
152	1992-11-30	9.5	7.385714	376.83
...	...	...	...	...
830	2005-11-28	5.9	2.714286	360.67
831	2005-12-05	7.1	3.157143	360.85
832	2005-12-12	10.2	3.200000	361.95
833	2005-12-19	12.8	2.514286	363.28
834	2005-12-26	15.3	-0.950000	364.93

687 rows × 4 columns

sns.pairplot(data[col2use], corner=True)
plt.show()

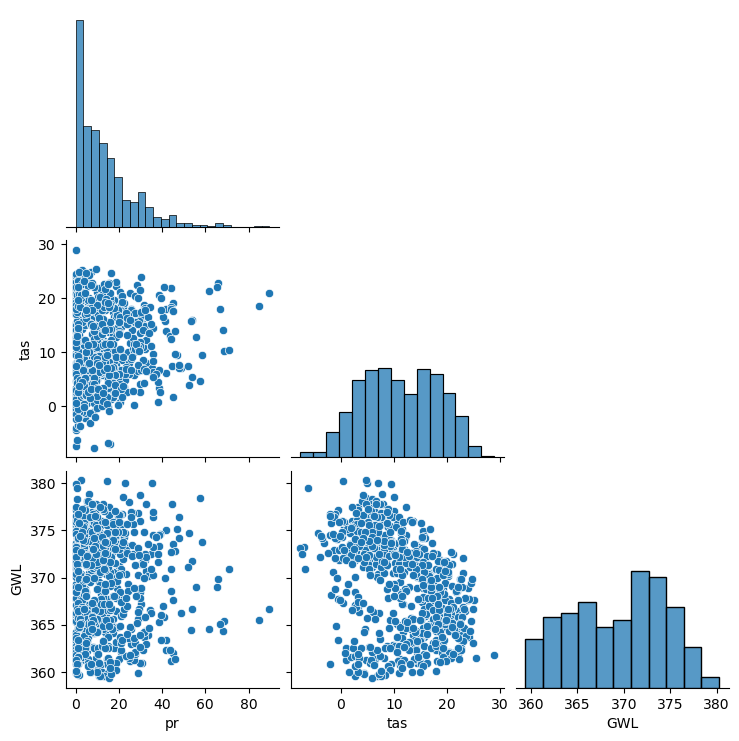
Nun integrieren wir in unseren Datensatz pro Grundwasserpegelwert die Niederschlags- (pr) und Temperaturwerte (tas) von jeweils 2, 5 und 10 Wochen im Vorhinein. Dieser Schritt ist wichtig, um die Präzision der Vorhersage zu verbessern. Der aktuelle Grundwasserpegel ist grundsätzlich auch abhängig von den Niederschlagswerten der vergangenen Wochen. Zudem kann die Temperatur der vergangenen Wochen auch ein Indikator für die Bodenfeuchte sein.

data["pr_sum_rolling_2w"] = data["pr"].rolling(2).sum()

data["pr_sum_rolling_5w"] = data["pr"].rolling(5).sum()

data["pr_sum_rolling_10w"] = data["pr"].rolling(10).sum()

data

	Date	pr	tas	GWL	pr_sum_rolling_2w	pr_sum_rolling_5w	pr_sum_rolling_10w
148	1992-11-02	10.2	7.900000	371.92	NaN	NaN	NaN
149	1992-11-09	35.0	6.800000	372.46	45.2	NaN	NaN
150	1992-11-16	22.8	6.914286	373.40	57.8	NaN	NaN
151	1992-11-23	21.6	8.500000	376.69	44.4	NaN	NaN
152	1992-11-30	9.5	7.385714	376.83	31.1	99.1	NaN
...	...	...	...	...	...	...	...
830	2005-11-28	5.9	2.714286	360.67	12.6	38.6	91.7
831	2005-12-05	7.1	3.157143	360.85	13.0	29.8	52.8
832	2005-12-12	10.2	3.200000	361.95	17.3	39.9	62.0
833	2005-12-19	12.8	2.514286	363.28	23.0	42.7	74.8
834	2005-12-26	15.3	-0.950000	364.93	28.1	51.3	84.5

687 rows × 7 columns

data["tas_sum_rolling_2w"] = data["tas"].rolling(2).sum()

data["tas_sum_rolling_5w"] = data["tas"].rolling(5).sum()

data["tas_sum_rolling_10w"] = data["tas"].rolling(10).sum()

data

	Date	pr	tas	GWL	pr_sum_rolling_2w	pr_sum_rolling_5w	pr_sum_rolling_10w	tas_sum_rolling_2w	tas_sum_rolling_5w	tas_sum_rolling_10w
148	1992-11-02	10.2	7.900000	371.92	NaN	NaN	NaN	NaN	NaN	NaN
149	1992-11-09	35.0	6.800000	372.46	45.2	NaN	NaN	14.700000	NaN	NaN
150	1992-11-16	22.8	6.914286	373.40	57.8	NaN	NaN	13.714286	NaN	NaN
151	1992-11-23	21.6	8.500000	376.69	44.4	NaN	NaN	15.414286	NaN	NaN
152	1992-11-30	9.5	7.385714	376.83	31.1	99.1	NaN	15.885714	37.500000	NaN
...	...	...	...	...	...	...	...	...	...	...
830	2005-11-28	5.9	2.714286	360.67	12.6	38.6	91.7	4.185714	26.485715	91.228571
831	2005-12-05	7.1	3.157143	360.85	13.0	29.8	52.8	5.871428	18.157143	80.500000
832	2005-12-12	10.2	3.200000	361.95	17.3	39.9	62.0	6.357143	13.842857	69.157143
833	2005-12-19	12.8	2.514286	363.28	23.0	42.7	74.8	5.714286	13.057143	59.800000
834	2005-12-26	15.3	-0.950000	364.93	28.1	51.3	84.5	1.564286	10.635714	47.421428

687 rows × 10 columns

2.1.2. Was ist ein Random Forest?

Ein Random Forest ist ein Ensemble-Lernverfahren, das aus vielen Entscheidungsbäumen besteht, die während des Trainings erstellt werden. Jeder Baum wird aus einem zufälligen Teil der Trainingsdaten und zufällig ausgewählten Features gebildet. Die Vorhersagen der einzelnen Bäume werden dann zu einer Gesamtvorhersage aggregiert, was die Genauigkeit erhöht und Überanpassung (Overfitting) reduziert. Random Forests sind robust, flexibel und können sowohl für Klassifikations- als auch für Regressionsaufgaben verwendet werden.

2.1.2.1. Schritt 1: Datensatz in Trainings- and Testdaten aufteilen

data = data.set_index(pd.DatetimeIndex(data['Date']))
del data['Date']

data

	pr	tas	GWL	pr_sum_rolling_2w	pr_sum_rolling_5w	pr_sum_rolling_10w	tas_sum_rolling_2w	tas_sum_rolling_5w	tas_sum_rolling_10w
Date
1992-11-02	10.2	7.900000	371.92	NaN	NaN	NaN	NaN	NaN	NaN
1992-11-09	35.0	6.800000	372.46	45.2	NaN	NaN	14.700000	NaN	NaN
1992-11-16	22.8	6.914286	373.40	57.8	NaN	NaN	13.714286	NaN	NaN
1992-11-23	21.6	8.500000	376.69	44.4	NaN	NaN	15.414286	NaN	NaN
1992-11-30	9.5	7.385714	376.83	31.1	99.1	NaN	15.885714	37.500000	NaN
...	...	...	...	...	...	...	...	...	...
2005-11-28	5.9	2.714286	360.67	12.6	38.6	91.7	4.185714	26.485715	91.228571
2005-12-05	7.1	3.157143	360.85	13.0	29.8	52.8	5.871428	18.157143	80.500000
2005-12-12	10.2	3.200000	361.95	17.3	39.9	62.0	6.357143	13.842857	69.157143
2005-12-19	12.8	2.514286	363.28	23.0	42.7	74.8	5.714286	13.057143	59.800000
2005-12-26	15.3	-0.950000	364.93	28.1	51.3	84.5	1.564286	10.635714	47.421428

687 rows × 9 columns

# Features und target trennen
X = data.drop(columns=['GWL'])
y = data['GWL']

# Daten in Trainings- und Testmengen aufteilen
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

2.1.2.2. Schritt 2: Initiales Modell trainieren

# Initialwert und Anzahl der Bäume für den Random Forest festlegen
seed = 196
n_estimators = 100

# RandomForest erstellen, X und y definieren und Modell trainieren
model = RandomForestRegressor(n_estimators = n_estimators, random_state = seed, max_features = 1.0,
                               min_samples_split = 2, min_samples_leaf = 1, max_depth = None)
model.fit(X_train, y_train)

RandomForestRegressor(random_state=196)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Die Zeile model.fit(X_train, y_train) startet den Trainingsprozess eines Random Forest Regressors, nachdem der Initialwert (Seed) und die Anzahl der Bäume festgelegt wurden. Die Parameter n_estimators und random_state legen die Anzahl der Entscheidungsbäume und den Zufallsstartwert fest. Weitere Parameter wie max_features, min_samples_split, min_samples_leaf und max_depth steuern die Struktur und die Komplexität der einzelnen Bäume. Während des Trainingsprozesses wird jeder Baum auf einem zufälligen Teil der Trainingsdaten (X_train, y_train) aufgebaut, wobei eine zufällige Auswahl von Merkmalen für die Splits verwendet wird. Durch die Aggregation der Vorhersagen aller Bäume wird ein robustes Modell erzeugt, das eine hohe Genauigkeit bei der Vorhersage ermöglicht und gleichzeitig Überanpassung (Overfitting) reduziert.

2.1.2.3. Schritt 3: Evaluieren

# Bestimmheitsmaß und erklärte Varianz ausgeben lassen
print(f"Coefficient of determination: {model.score(X_train, y_train)}")
print(f"% Var explained: {model.score(X_train, y_train) * 100}")

Coefficient of determination: 0.9530484749262945
% Var explained: 95.30484749262945

In diesem Codeabschnitt werden 2 wichtige Leistungskennzahlen für das Modell ausgegeben: das Bestimmtheitsmaß und die erklärte Varianz.

Zusammengefasst gibt das Bestimmtheitsmaß bzw. die erklärte Varianz Auskunft darüber, wie gut ein Modell die Streuung der Daten erklärt. Ein höheres Bestimmtheitsmaß deutet auf ein besseres Modell hin, das die Daten gut beschreibt. Unser Ergebnis von ca. 0.95 suggeriert eine hohe Vorhersagegenauigkeit.

y_predictions = model.predict(X_test)

# Import library for metrics
from sklearn.metrics import mean_squared_error, r2_score, mean_absolute_error
# Mean absolute error (MAE)
mae = mean_absolute_error(y_test, y_predictions)
# Mean squared error (MSE)
mse = mean_squared_error(y_test, y_predictions)
# R-squared scores
r2 = r2_score(y_test, y_predictions)

mae, mse, r2

(2.0546712560386524, 8.391051875257594, 0.6901583928593296)

In diesem Codeabschnitt werden Vorhersagen für die Testdaten erstellt. Diese Vorhersagen werden dann mit den tatsächlichen Werten verglichen und im Anschluss der durchschnittliche absolute Fehler, der durchschnittliche quadrierte Fehler und das Bestmmtheistmaß berechnet. Im Durchschnitt weichen die Vorhersagen des Modells um etwa 2,05 Einheiten (hier Meter ü. NN) von den tatsächlichen Werten ab. Ein R²-Wert von 0,69 bedeutet, dass etwa 69 % der Varianz in den tatsächlichen Werten durch das Modell erklärt werden.

data

	pr	tas	GWL	pr_sum_rolling_2w	pr_sum_rolling_5w	pr_sum_rolling_10w	tas_sum_rolling_2w	tas_sum_rolling_5w	tas_sum_rolling_10w
Date
1992-11-02	10.2	7.900000	371.92	NaN	NaN	NaN	NaN	NaN	NaN
1992-11-09	35.0	6.800000	372.46	45.2	NaN	NaN	14.700000	NaN	NaN
1992-11-16	22.8	6.914286	373.40	57.8	NaN	NaN	13.714286	NaN	NaN
1992-11-23	21.6	8.500000	376.69	44.4	NaN	NaN	15.414286	NaN	NaN
1992-11-30	9.5	7.385714	376.83	31.1	99.1	NaN	15.885714	37.500000	NaN
...	...	...	...	...	...	...	...	...	...
2005-11-28	5.9	2.714286	360.67	12.6	38.6	91.7	4.185714	26.485715	91.228571
2005-12-05	7.1	3.157143	360.85	13.0	29.8	52.8	5.871428	18.157143	80.500000
2005-12-12	10.2	3.200000	361.95	17.3	39.9	62.0	6.357143	13.842857	69.157143
2005-12-19	12.8	2.514286	363.28	23.0	42.7	74.8	5.714286	13.057143	59.800000
2005-12-26	15.3	-0.950000	364.93	28.1	51.3	84.5	1.564286	10.635714	47.421428

687 rows × 9 columns

Allerdings könnten unsere Ergebnisse auch an der Auswahl der Trainings- und Testdaten liegen. Um den Einfluss dieser Aufteilung zu reduzieren, führen wir eine sogenannte k-fache Kreuzvalidierung (k-fold cross validation) durch. Das bedeutet, dass wir die Trainingsdaten in 10 gleich große Teile aufteilen, also \(k=10\) in diesem Fall. Dann trainieren wir das Modell auf neun der 10 Teile und verwenden den 10. Teil zur Validierung des Modells wie oben beschrieben. Dieser Prozess wird 10 Mal wiederholt, wobei jedes Mal ein anderer Teil zur Validierung verwendet wird. Am Ende erhalten wir 10 RMSE-Werte, die uns einen Einblick in die Validität des oben genannten Wertes geben.

from sklearn.model_selection import cross_val_score
scores = - cross_val_score(estimator=model, X=X_train, y=y_train, cv=10, scoring='neg_mean_squared_error', n_jobs=1)
print(scores)
print(np.mean(scores), np.std(scores))

[ 7.99462509  7.6769795   8.86374395  7.83255243  9.20695896 10.75050609
  6.92620051  9.73670632  8.32539769 10.4834025 ]
8.779707304687633 1.1942959488195237

2.1.2.4. Schritt 4: Hyperparameter Tuning

Hier verwenden wir Grid Search, um die besten Hyperparameter für unser Modell zu finden. Hyperparameter sind Parameter, die nicht durch das Modelltraining selbst optimiert werden, sondern im Vorhinein festgelegt werden müssen. Sie steuern die Lernprozesse und die Architektur des Modells. Im Gegensatz zu Modellparametern, die während des Trainings durch Optimierungsalgorithmen angepasst werden, werden Hyperparameter manuell oder automatisiert (z. B. durch Grid Search) bestimmt. Grid Search durchsucht systematisch einen vordefinierten Bereich von Hyperparametern und evaluiert die Modellleistung für jede Kombination. Dies ermöglicht es, die optimalen Hyperparameter auszuwählen, die die Modellleistung maximieren und somit zu besseren Vorhersagen führen.

2.1.2.4.1. gridSearchCV

from sklearn.model_selection import GridSearchCV

rfc = RandomForestRegressor(random_state=42)

param_grid = { 
    'n_estimators': [50, 100, 150, 200, 250, 300],
   # 'max_features': ['auto', 'sqrt', 'log2'],
    'max_depth' : [4,5,6,7,8],
#    'criterion' :['gini', 'entropy']
}

CV_rfc = GridSearchCV(estimator=rfc, param_grid=param_grid, cv= 5)
CV_rfc.fit(X_train, y_train)

GridSearchCV(cv=5, estimator=RandomForestRegressor(random_state=42),
             param_grid={'max_depth': [4, 5, 6, 7, 8],
                         'n_estimators': [50, 100, 150, 200, 250, 300]})

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

best_params = CV_rfc.best_params_

best_params

{'max_depth': 8, 'n_estimators': 150}

Der Hyperparameter max_depth bestimmt die maximale Tiefe der Entscheidungsbäume im Random Forest-Modell. Eine Tiefe von 8 bedeutet, dass jeder Baum im Random Forest maximal 8 Ebenen tief ist. Der Hyperparameter n_estimators gibt die Anzahl der Entscheidungsbäume im Random Forest-Modell an. In diesem Fall bedeutet n_estimators: 150, dass der Random Forest aus 150 Entscheidungsbäumen besteht.

# Initialwert für den Random Forest festlegen
seed = 196


# RandomForest erstellen, X und y definieren und Modell trainieren
model = RandomForestRegressor(n_estimators = best_params["n_estimators"], 
                              random_state = seed, 
                              max_features = 1.0,
                              min_samples_split = 2, 
                              min_samples_leaf = 1, 
                              max_depth = best_params["max_depth"])
model.fit(X_train, y_train)

RandomForestRegressor(max_depth=8, n_estimators=150, random_state=196)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

X_train

	pr	tas	pr_sum_rolling_2w	pr_sum_rolling_5w	pr_sum_rolling_10w	tas_sum_rolling_2w	tas_sum_rolling_5w	tas_sum_rolling_10w
Date
1998-03-02	24.1	9.985715	26.400000	42.100000	95.700000	17.271429	30.771429	48.042858
1994-12-12	2.8	5.185714	8.900000	50.900000	79.000000	13.685714	38.842857	87.999999
1994-05-30	12.2	15.957143	33.100000	120.300000	196.299999	30.742857	76.385714	128.299999
1993-10-25	0.0	4.757142	20.100000	74.999999	155.799999	11.185713	47.914285	123.228570
1997-01-06	0.0	-3.971428	8.700000	55.899998	169.199998	-11.628571	-14.571429	11.257143
...	...	...	...	...	...	...	...	...
1994-03-14	18.7	7.628571	32.300000	55.200000	98.300000	17.528572	28.728572	48.328572
1994-11-14	16.4	10.528571	25.800000	44.500000	110.500000	19.814285	49.799999	111.528569
1998-01-05	7.0	6.714286	23.400000	76.100000	145.900000	13.614286	28.142858	52.828572
2001-03-05	10.6	8.071428	21.899999	49.299999	122.699997	11.242857	28.728571	44.385714
1994-10-17	3.2	8.685714	3.200000	35.800000	152.700000	18.571428	56.799998	140.028566

549 rows × 8 columns

2.1.2.5. Schritt 5: Plotten

stats = model.get_params()
feature_importance = model.feature_importances_
features = X.columns
var_imp_df = pd.DataFrame({'Feature': features, 'Importance': feature_importance})
var_imp_df = var_imp_df.sort_values(by = 'Importance', ascending = False).head(54)
var_imp_10 = var_imp_df.head(10)

# Plotten der wichtigsten Variablen
plt.figure(figsize = (8, 3))
sns.barplot(x = 'Importance', y = 'Feature', data = var_imp_10, color = 'pink')
plt.title("δ¹⁸O")
plt.xlabel("Importance score")
plt.ylabel("Feature")
plt.text(0, -1.5, f"n_estimators = {n_estimators}, max_features = {max_features}\nRMSE = {rmse:.2f}, R² = {r2:.2f}", 
         fontsize = 10, ha = 'left', va = 'center')
plt.show()

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[373], line 7
      5 plt.xlabel("Importance score")
      6 plt.ylabel("Feature")
----> 7 plt.text(0, -1.5, f"n_estimators = {n_estimators}, max_features = {max_features}\nRMSE = {rmse:.2f}, R² = {r2:.2f}", 
      8          fontsize = 10, ha = 'left', va = 'center')
      9 plt.show()

NameError: name 'max_features' is not defined

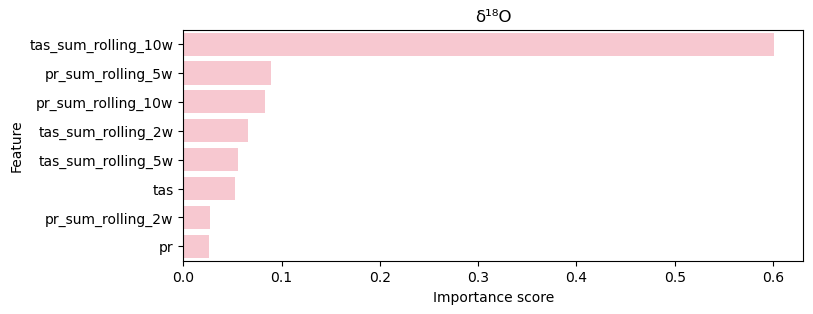
Hierbei ist klar geworden, dass die Variable der Temperatur 10 Wochen im Vorhinein die Wichtigste ist.

data_1992_2004 = data[(data.index.year >= 1992) & (data.index.year <= 2004)]
data_2005 = data[(data.index.year >= 2005)]

data.index.year

Index([1992, 1992, 1992, 1992, 1992, 1992, 1992, 1992, 1992, 1993,
       ...
       2005, 2005, 2005, 2005, 2005, 2005, 2005, 2005, 2005, 2005],
      dtype='int32', name='Date', length=687)

data_1992_2004

	pr	tas	GWL	pr_sum_rolling_2w	pr_sum_rolling_5w	pr_sum_rolling_10w	tas_sum_rolling_2w	tas_sum_rolling_5w	tas_sum_rolling_10w
Date
1992-11-02	10.2	7.900000	371.92	NaN	NaN	NaN	NaN	NaN	NaN
1992-11-09	35.0	6.800000	372.46	45.2	NaN	NaN	14.700000	NaN	NaN
1992-11-16	22.8	6.914286	373.40	57.8	NaN	NaN	13.714286	NaN	NaN
1992-11-23	21.6	8.500000	376.69	44.4	NaN	NaN	15.414286	NaN	NaN
1992-11-30	9.5	7.385714	376.83	31.1	99.1	NaN	15.885714	37.500000	NaN
...	...	...	...	...	...	...	...	...	...
2004-11-29	3.1	4.457143	374.78	7.5	41.0	120.200002	9.771429	27.157143	87.857143
2004-12-06	0.0	0.528571	372.96	3.1	36.2	107.200002	4.985714	17.628572	74.271429
2004-12-13	12.5	1.028571	371.89	12.5	27.7	99.500002	1.557143	15.457143	61.714286
2004-12-20	4.6	2.157143	371.48	17.1	24.6	90.500002	3.185714	13.485715	54.757144
2004-12-27	12.6	3.357143	373.36	17.2	32.8	98.600002	5.514286	11.528572	45.842858

635 rows × 9 columns

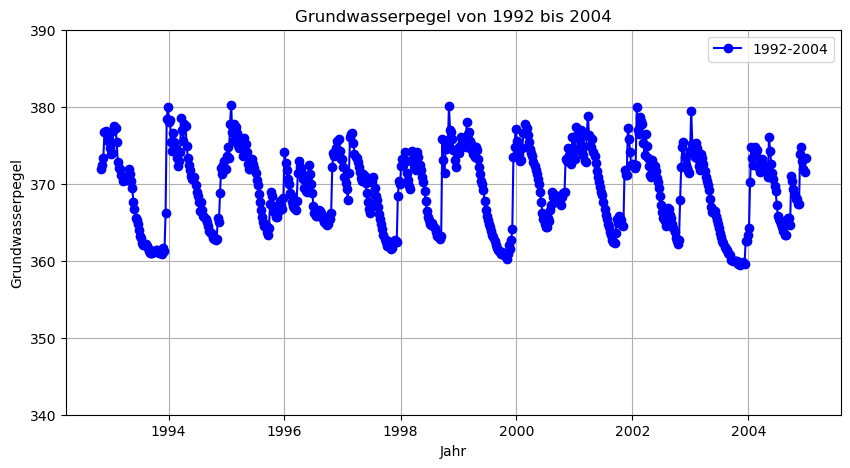
# Daten zwischen 1992 und 2004 plotten

plt.figure(figsize=(10, 5))
plt.plot(data_1992_2004.index, data_1992_2004['GWL'], marker='o', linestyle='-', color='b', label='1992-2004')
plt.xlabel('Jahr')
plt.ylabel('Grundwasserpegel')
plt.title('Grundwasserpegel von 1992 bis 2004')
plt.legend()
plt.grid(True)
plt.ylim(340, 390) 
plt.show()

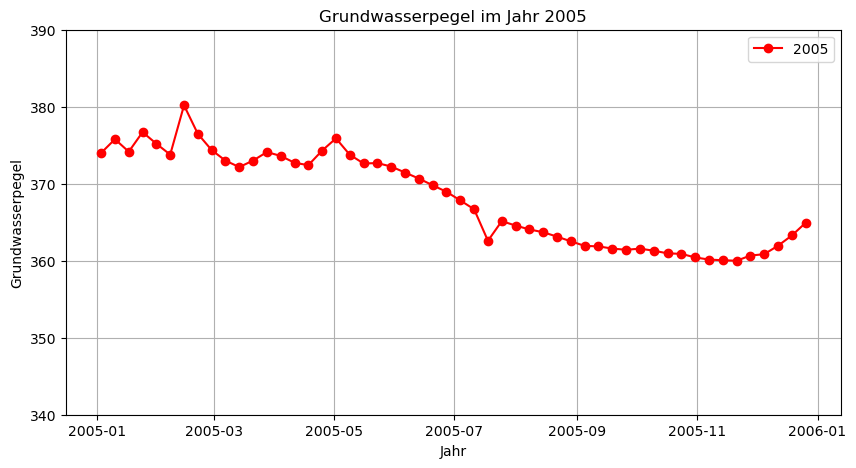
# Daten von 2005 plotten

plt.figure(figsize=(10, 5))
plt.plot(data_2005.index, data_2005['GWL'], marker='o', linestyle='-', color='r', label='2005')
plt.xlabel('Jahr')
plt.ylabel('Grundwasserpegel')
plt.title('Grundwasserpegel im Jahr 2005')
plt.legend()
plt.grid(True)
plt.ylim(340, 390)  
plt.show()

X_val, y_val=data_2005.drop(columns=['GWL']), data_2005['GWL']

y_predictions_2005 = model.predict(X_val) 

# Die Vorhersagewerte und die tatsächlichen Werte aus 2005 gleichzeitig plotte, um Modelleistung zu sehen. 
plt.plot(X_val.index, y_predictions_2005, marker='o', linestyle='-', color = 'red', label = 'Vorhersagewerte')
plt.plot(X_val.index, y_val, marker='o', linestyle='-', color = 'green', label = 'tatsächliche Werte')
plt.xlabel('Jahr')
plt.ylabel('Grundwasserpegel')
plt.title('Grundwasserpegel im Jahr 2005')
plt.legend()
plt.show()

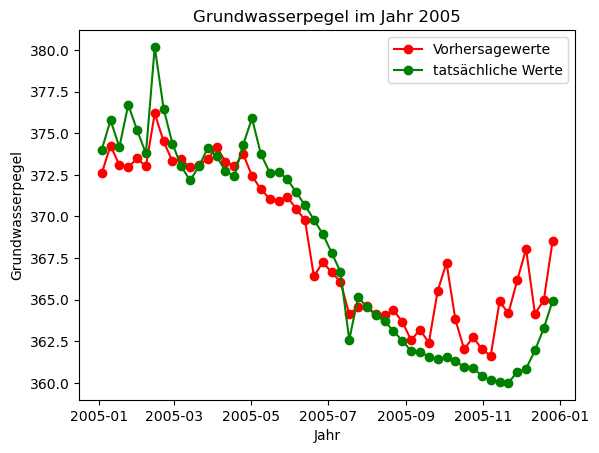
Hierbei stellt der rote Graph die vom Modell vorhergesagten Were an, wobei der grüne Graph die tatsächlichen Daten von 2005 darstellt. Wir sehen, dass die Diskrepanzen zwischen den 2 Graphen relativ klein sind.

2.1.3. Diskussion

Zusammenfassend haben wir hier ein Random-Forest-Modell entwickelt, um die Grundwasserstände an der Messstelle Lettgenbrunn in Hessen vorherzusagen. Dafür wurden die Grundwasserdaten der Messstelle, sowie die Temperatur- und Niederschlagsdaten für den Zeitraum von 1992 bis 2005 gesammelt und in das Modell eingespeist. Die Entscheidung, die Vorhersage auf eine einzelne Messstelle zu beschränken, wurde getroffen, um Overfitting zu vermeiden. Anfangs hatten wir versucht, die Daten mehrerer Messstellen zu aggregieren, jedoch führte dies zu einer geringeren Modellleistung. Dies lag wahrscheinlich an der hohen Heterogenität der Daten, insbesondere der Niederschlags- und Temperaturwerte, die stark zwischen den verschiedenen Messstellen variierten.

Ein wesentlicher Schritt zur Verbesserung der Modellgenauigkeit war die Erweiterung der Features um historische Daten. Neben den aktuellen Temperatur- und Niederschlagswerten wurden auch die Werte von 2, 5 und 10 Wochen zuvor einbezogen. Diese Erweiterung der Features hat sich als vorteilhaft erwiesen, da Temperatur- und Niederschlagswerte wichtige Indikatoren für die Bodenfeuchte sind und historische Werte einen bedeutenden Einfluss auf den aktuellen Grundwasserstand haben. Die Integration dieser zusätzlichen Datenpunkte hat die Vorhersagegenauigkeit deutlich verbessert.

Das Modell erzielte bei den Trainingswerten ein Bestimmtheitsmaß (R²) bzw. eine erklärte Varianz von ca. 95%, was auf eine gute Modellleistung hinweist. Bei den Testdaten erreichte das Modell ein Bestimmheitsmaß von ca. 69%. Zur Validierung des Modells wurden die vorhergesagten Grundwasserstände für das Jahr 2005 mit den tatsächlichen Werten verglichen. Die simultane Darstellung beider Datensätze in einem Plot zeigte, dass die vorhergesagten Werte den tatsächlichen Werten ziemlich nahe kamen.

Trotzdem beobachten wir, dass die Vorhersage fehlerhaft ist. Besonders im Umgang mit extremen Werten, scheint das Modell Fehler zu machen. Ein möglicher Grund hierfür könnte die Komplexität von Grundwasserdaten generell und die limitierte Datenverfügbarkeit sein. Grundwasserstände werden von zahlreichen Faktoren beeinflusst, die in komplexen, nichtlinearen Beziehungen zueinander stehen. Einflussfaktoren wie die Bodenbeschaffenheit, anthropogene Einflüsse, die Landnutzung und die Vegetation wurden bei unserem Modell außer Acht gelassen. Die Intergration der genannten Einflussfaktoren in den Datensatz hätte vermutlich ein genaueres Vorhersagergebnis erzielt. Ferner neigen Random Forest-Modelle dazu, extremere Werte zu glätten, da sie auf dem Durchschnitt vieler Entscheidungsbäume basieren und extreme Ausprägungen in den Entscheidungsbäumen in den Mittelwert miteinfließen. Dies kann dazu führen, dass Extremwerte flacher vorausgesagt werden, als sie tatsächlich sind, wie das in unserem Modell bis ca. August 2005 der Fall ist. Unser Modell ist etwas überangepasst (overfittet), was durch die Diskrepanz zwischen den erklärten Varianzen der Trainings- und Testdaten gezeigt wird. Dies spiegelt sich in der teilweise Ungenauigkeit unserer Vorhersage wider. Außerdem sagt das Modell die Fluktuationen zum Teil extremer voraus, als sie eigentlich sind, z.B. zwischen September und November 2005. Dies könnte daran liegen, dass in den Trainingsdaten die Fluktuationen zum Ende des Jahres tendenziell extremer waren, also Extremwerte überrepräsentiert waren und das Modell diese Extremwerte in der Vorhersage überbetont.

Insgesamt zeigt die Modellleistung jedoch, dass der Random Forest eine leistungsfähige Methode zur Vorhersage von Grundwasserständen ist, insbesondere wenn relevante historische Daten einbezogen werden. Weitere Verfeinerungen des Modells und eine erweiterte Datengrundlage um weitere Eiflussfaktoren für Gundwasserstände könnten die Vorhersagegenauigkeit weiter verbessern.